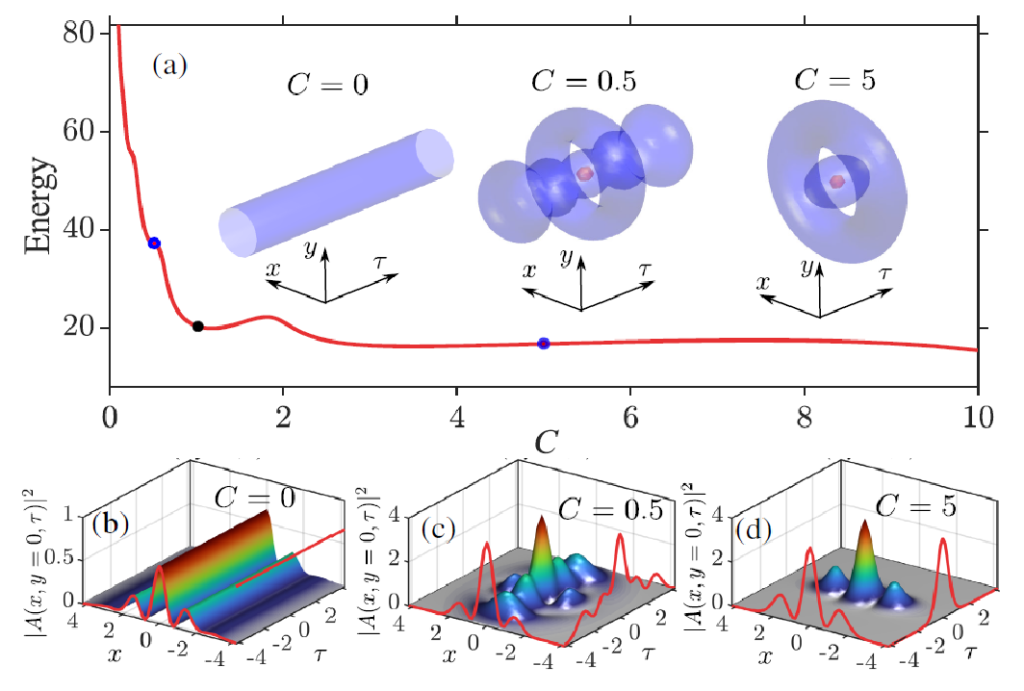
We present a general approach to excite robust dissipative three-dimensional and high-order solitons and breathers in passively driven nonlinear cavities. Our findings are illustrated in the paradigmatic example provided by an optical Kerr cavity with diffraction and anomalous dispersion, with the addition of an attractive three-dimensional parabolic potential. The potential breaks the translational symmetry along all directions, and impacts the system in a qualitatively unexpected manner: three-dimensional solitons, or light bullets, are the only existing and stable states for a given set of parameters. This property is extremely rare, if not unknown, in passive nonlinear systems. As a result, the excitation of the cavity with any input field leads to the deterministic formation of a target soliton or breather, with a spatiotemporal profile that unambiguously corresponds to the given cavity and pumping conditions. In addition, the tuning of the potential width along the temporal direction results in the existence of a plethora of stable asymmetric solitons. Our results may provide a solid route toward the observation of dissipative light bullets and threedimensional breathers.
