The spatiotemporal nature of nonlinear mode coupling in graded index (GRIN) is responsible for the experimental observation of multimode solitons [1]. Work by Krupa et al. [2] has more recently shown that the Kerr effect in GRIN fibers may lead to highly stable beam self cleaning for sub-ns pulses. Temporal pulse compression with Kerr beam cleaning was already observed in the highly dispersive regime with fs pulses in Ref. [3]. In this work, we experimentally and numerically analyze the complex nonlinear evolution of self-cleaned beams in the temporal domain by direct detection of quasi-CW pulses in normal dispersion regime and when the dispersion length is much longer than the fiber length [4].

Our experiments were carried out with an amplified microchip Q-switched laser delivering 740 ps pulses at a repetition rate of 27 kHz, with a central wavelength of 1064 nm. The maximum energy per pulse can reach more than 100 mJ, with a peak power level up to 150 kW. The optical beam with 40 mm diameter was coupled into a 12-m long GRIN 50/125 multimode silica fiber. A fast In-GaAs PIN photodiode was connected to a 20-GHz bandwidth oscilloscope and used to measure the output pulse envelope with samples spaced by 25 ps. The photodiode had an active area 150 times smaller than the area of the imaged near field, which was properly magnified. The experimental results when the photodiode was placed at the center of the near-field image are shown in panel (a) of Fig.1 . Upon increases of the input power, the temporal reshaping of the pulse envelope was observed to exhibit a complex behaviour, composed by a series of temporal broadenings, followed by the formation of a dip at the pulse center and then the growth of a narrower and high power peak.

Since in our case the effect of dispersion is negligible, the long pulse can be modeled as a sequence of different instantaneous power values, and the nonlinear evolution of the corresponding modal amplitudes is described by standard coupled mode equations [4]. From these equations, it is possible to calculate the input-output transmission ratio of the fundamental mode (whose intensity is located in the center of the beam) upon power.

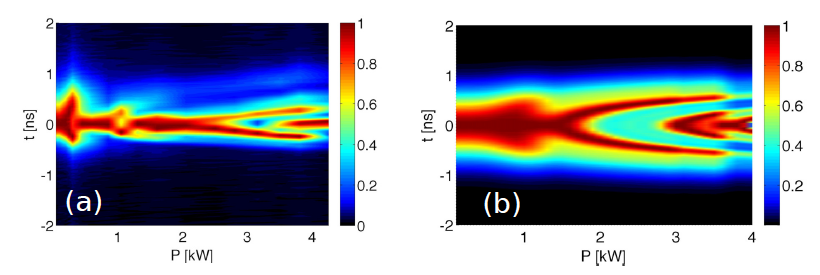
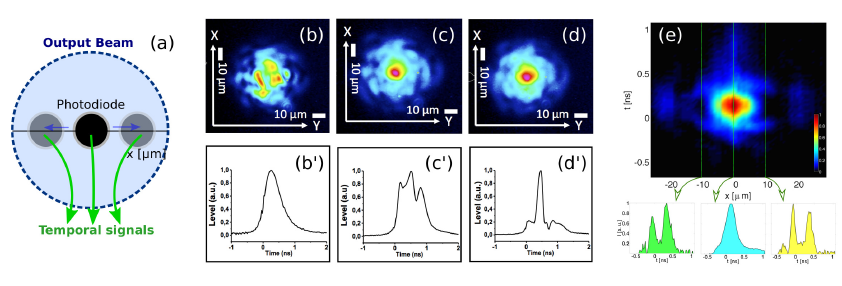
The numerical study (panel (b) of Fig.1) of the transmission into the fundamental mode upon peak power has features similar to experiments including the dip and the temporal narrowing. Additional experimental results are illustrated in Fig.2: panel (a) outlines the moving of the position of the photodiode across the output near-field image. Panels (b)-(d) show the progress of beam cleaning when increasing input beam power. Panels (b’)-(d’) show the corresponding temporal waveforms when the photodiode is placed at the center of the image x = 0. Note that in panel (d’) the temporal duration reduces to 175 ps.

Panel (e) shows a collection of temporal waveforms (including some selected profiles) for different positions of the photodiode at 2kW. As can be seen the central part of the output beam is carried by a common temporal envelope. On the other hand temporal dips are observed when the photodiode is offset by about 10 microns from the beam center, when the image is rescaled to the size of the fiber core.

In conclusion, we have shown experimentally that spatiotemporal mode coupling in nonlinear GRIN fibers may enable the simultaneous cleanup and temporal reshaping, which may result into a strong reduction of the pulse duration for a sub-ns pulse. These results may have important applications in the development of high power mode-locked fiber lasers based on multimode optical fibers.

1. W. H. Renninger and F. W. Wise,“Optical solitons in graded-index multimode fibres,” Nat. Commun. 11, 1719 (2012).
2. K.Krupa, A.Tonello, B.M. Shalaby, M. Fabert, A. Barth´el´emy, G. Millot, S. Wabnitz, and V. Couderc, “Spatial beam self-cleaning in multimode fibre,” Nat. Photon. 11, 234–241 (2017).
3. Z. Liu, L. G. Wright, D. N. Christodoulides and Frank W. Wise, “Kerr self-cleaning of femtosecond-pulsed beams in graded-index multimode fiber,” Opt. Lett. 16, 3675–3678 (2016).
4. K. Krupa, A. Tonello, V. Couderc, A. Barth´el´emy, G. Millot, D. Modotto, S. Wabnitz, “Spatiotemporal light beam compression from complex nonlinear mode mixing,” arXiv:1711.11478.