When propagating along a multimode fiber, light is affected by random linear coupling caused by stress, bending, or technological irregularities of the fiber. This leads to a rapid distortion of the spatial intensity profile of the input beam, and to the appearance of highly speckled structures at the fiber output. Recent experiments have demonstrated that the Kerr effect in a graded-index (GRIN) MMFs can overcome such speckle distortions, leading to the spatial beam self-cleaning effect. As a result, one obtains a robust bell-shaped nonlinear beam, which at the fiber output has a diameter close to that the fundamental mode.

Ww numerically investigate the process of Kerr beam self-cleaning in GRIN MMFs. Unlike previous approaches, where the nonlinear propagation of a spatial beam along an optical fiber was described by the generalized 3D nonlinear Schrödinger equation, in this work we use the coupled-mode model. In order to take into account the presence of various imperfections of the fiber, we added a random linear coupling between modes to the nonlinear coupled mode model. How various fiber imperfections impact linear mode coupling in MMFs still remains an active topic of investigation. Therefore, in our work we considered various types of linear mode coupling, and investigated their effects on the beam self-cleaning process.

In our study, we consider a 62.5 μm GRIN fiber. At the fiber input, we suppose to launch a Gaussian beam of a certain radius at , and at the wavelength of 1064 nm. First we need to decompose the input beam into modes, thereby setting the initial modal power distribution: we assume that the input beam has a constant phase distribution over the xy plane. In our simulations, we consider up to 153 spatial modes.

First, we considered the case in which all spatial modes are linearly coupled to each other, and the limdear mode coupling coefficients are random variables that change with each integration step. This may be caused by various fiber imperfections, resulting in random fluctuations in the refractive index of the core, or in the core diameter, and corresponds to a strong coupling regime between all modes. With this type of coupling, the energy of each mode oscillates rapidly during the propagation, but on average it varies slightly. Therefore, when using the model with random linear coupling between all spatial modes, we cannot observe a speckle pattern at the output of the fiber.

Next, we considered a model in which only modes with adjacent (radial and azimuthal) mode numbers are coupled. Such a model may correspond to the case of fiber tilting, in which energy can be transfered only among neighbouring modes in the linear regime. In this case, although the beam at the fiber output is distorted, it does not appear to reproduce the highly speckled field which is obtained in experiments. In addition, rapid oscillations of the fundamental mode power are observed.

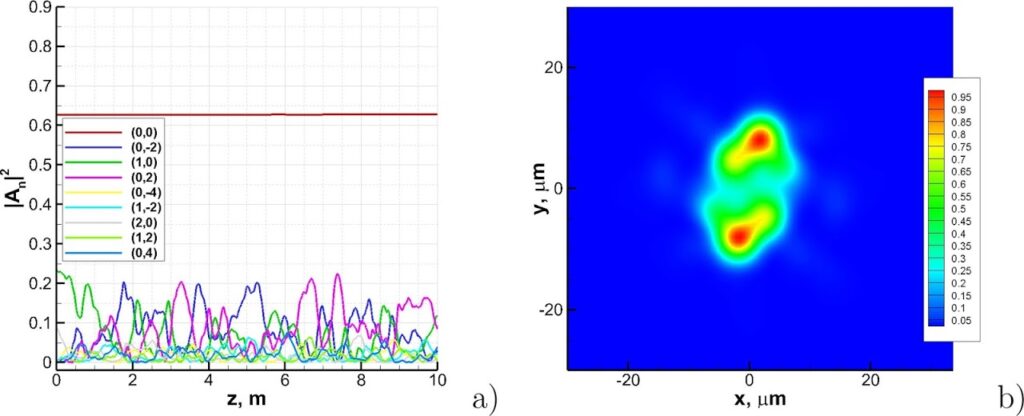
Finally, we considered a model with random linear coupling between spatial modes with equal mode numbers n only. In this case, only degenerate modes are linearly coupled, and the energy from the fundamental mode flows into azimuthal modes with the same number. Fig.1 shows the spatial dynamics of the energy distribution among the modes and the output field for an initial beam with a radius of 15 μm, and a power of 10 W. In this case, we can see an intense exchange of energy between the modes, while the power of the fundamental mode does not change. As we can see, the output beam exhibits a speckled pattern.

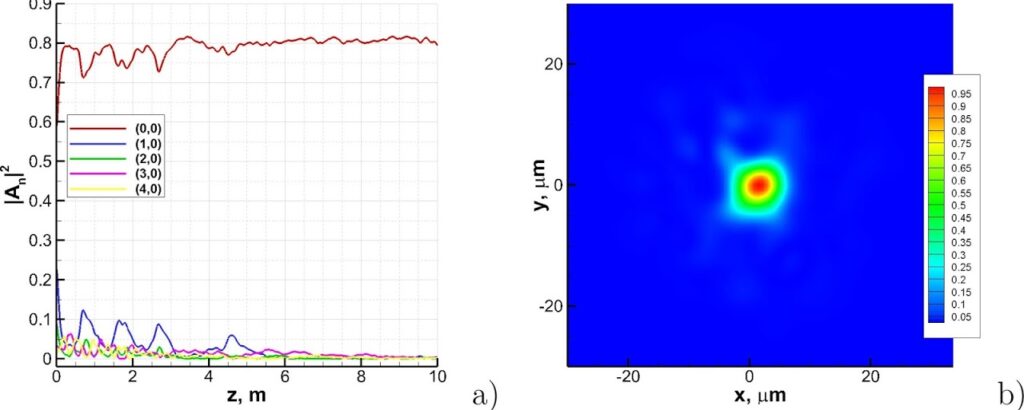
On the other hand, Fig. 2 shows the spatial dynamics of the energy distribution among modes, and the output field, for an initial beam with a radius of 15 μm, and a power of 10 kW, laterally shifted by 5 μm, obtained by a numerical solution of the coupled mode model with random linear coupling between modes with equal mode numbers only. In this case, one readily observes the appearance of a self-cleaning effect, and the fundamental mode power swiftly stabilizes upon propagation. The output beam for the considered model has a size that is close to that of the fundamental mode.