Multimode fibers (MMFs) have recently attracted considerable interest, motivated by their potential for increasing the transmission capacity of long-distance optical links via the technique of mode-division-multiplexing (MDM), which exploits the multiple transverse modes of the fiber as information carriers, and by their increased tolerance to high signal powers. Multimode graded-index optical fibers (GRIN MMFs) are commonly considered capable of supporting spatiotemporal solitons over long distances [1,2]. Theoretical treatments of spatiotemporal soliton propagation in MMFs mostly rely on the variational approach (VA) [3,4]. When neglecting the temporal dimension, the variational method permits to include the Kerr effect in the description of periodic spatial self-imaging (SSI), which occurs in GRIN MMFs [5-7]. Based on the VA, and by adding group-velocity dispersion, it has been proposed that soliton propagation in MMFs can be theoretically described in terms of a reduced one-dimensional generalized nonlinear Schrödinger equation (GNLSE) with a spatially varying effective mode area [8]. The validity of the VA is based on the assumption that the initial beam shape is maintained unchanged upon propagation, except for a limited set of slowly-varying parameters (e.g., the beam amplitude and width).

In our work we presented the experimental evidence, supported by numerical simulations, that an initially excited multimode femtosecond soliton, composed by a few low-order transverse modes, irreversibly decays into a singlemode soliton, owing to the FWM-induced energy transfer of higher-order modes into the fundamental mode of the MMF. Once formed, the singlemode soliton propagates stably over the tested fiber lengths of up to 1 km, which corresponds to the record transmission distance in a MMF of 4600 modal dispersion distances, and 5600 chromatic dispersion lengths. This effect is of particular importance for technological applications, since it reveals that nonlinearity can counteract the effects of modal dispersion and random mode coupling, and enables the stable  transport of high spatial quality beams over long distances by means of large area MMFs. As a side aspect, our results invalidate theoretical predictions based on the VA, since the beam shape substantially evolves along the fiber, in such a way that the initial beam profile is not maintained.

2.  Numerical simulations

We used a numerical model suitable for studying the propagation of multimodal pulses over long spans of GRIN fiber, based on the coupled-mode equations [9,10]. This requires a preliminary knowledge of the power distribution among the fiber modes at fiber input. The model couples the fields of propagating modes via Kerr and Raman nonlinearity, through four-wave mixing (FWM) terms of the type  Q_plmnA_lA_mA_n^*, being Q_plmn the coupling coefficients proportional to the overlap integrals of the transverse modal field distributions. The lack of symmetry between coupling coefficients is responsible for a slow, but irreversible transfer of energy from higher-order modes towards the fundamental, when pulses carried by different modes are temporally and spatially overlapping.

Fig. 1 shows the simulated energy (left) and wavelength (right) evolution of the propagating modes (1,0) or LP₀₁, (2,0) or LP₀₂, (3,0) or LP_03, when coupling at the fiber input a Gaussian pulse with 67 fs pulsewidth, 1550 nm wavelength, 30 µm diameter, and optimal peak power of 28 kW, which is suitable for spatiotemporal soliton generation.

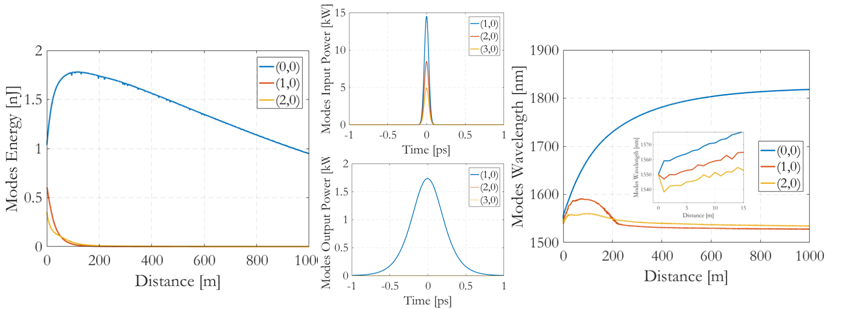
Fig. 1. Numerical simulation of 3 axial modes propagating over 1 km of GRIN fiber.

The top-center inset shows the input power time profile of the 3 modes. During the propagation over the first 10 meters of fiber, nonlinearity forces the carrier wavelengths of the 3 modes to split, so that pulses in different modes experience different chromatic dispersions, in order to compensate for modal dispersion walk-off. As a result, a spatiotemporal soliton is formed: the 3 modes remain trapped with each other, and propagate with the same speed. However, as a result of its nonlinear coupling with higher-order axial modes, after approximately 120 m of propagation the fundamental mode acts as an attractor, and it nearly completely absorbs energy carried by the other two modes. Higher-order modes degenerate into dispersive waves with negligible power, and a wavelength close to the initial value. In the subsequent 880 m of propagation, a substantially monomodal soliton propagates, experiencing a wavelength shift caused by Raman soliton self-frequency shift (SSFS). As the soliton wavelength increases above 1700 nm, it starts losing power by linear attenuation, and it adiabatically broadens in time, in order to preserve the monomodal solitonic condition (bottom-center inset).

3.  Experimental evidence

The simulation of Fig. 1 has shown that, for sufficiently short input pulses, a spatiotemporal soliton is formed after a few dispersion lengths, and the temporally trapped modes experience an irreversible transfer of energy towards the fundamental mode. After hundreds of dispersion/nonlinearity lengths, a singlemode soliton is formed, and it propagates in a stable manner.

In order to experimentally confirm the generation of monomodal solitons over long spans of GRIN multimodal fiber, a test-bed was prepared by using femtosecond pulses propagating over 120 m of fiber; the distance was chosen based on the results of Fig.1, indicating that a monomodal soliton is formed at that distance. The experimental setup used for the generation of MM solitons consists of an ultra-short laser system, including a hybrid optical parametric amplifier (OPA) of white-light continuum (Lightconversion ORPHEUS-F), pumped by a femtosecond Yb-based laser (Lightconversion PHAROS-SP-HP), generating pulses at 100 kHz repetition rate with Gaussian beam shape (M²=1.3); pulse temporal shape at 1550 nm is Gaussian with 67 fs pulsewidth. The laser beam is focused by a 50 mm lens into the fiber, with 1/e² input diameter of approximately 30 µm. The laser pulses enter the fiber with a peak power ranging between 100 W and 500 kW, adjusted by means of an external attenuator. The used fiber is a span of commercial parabolic GRIN fiber, with core radius r_c=25 µm, cladding radius 62.5µm, cladding index n_clad=1.444, relative index difference Δ=0.0103. At the fiber output, spectral and temporal profiles, as well as the beam near-field were collected.

Fig. 2 shows an example of measured autocorrelation traces (top row), beam near-field (central row), and spectra (bottom row) after 120 m of fiber transmission, for input pulse peak powers corresponding to: a) 22 kW (pre-soliton regime), b) 29 kW (soliton regime), c) 37 kW (soliton regime with Raman SSFS), d) 109 kW (multiple soliton generation), respectively. The experimental data confirm the generation of a pulse with minimum duration at the solitonic power (25-30 kW input peak power). The output spectra show sech-shaped lobes, suffering SSFS shift up to the wavelength of linear absorption, near 2100 nm. As can be seen, the output beam reaches its minimum waist at the same power value for minimum pulsewidth; the beam waist reduces to 8.5 µm, close to the 7.7 µm theoretical value for the fundamental mode beam in a GRIN fiber, confirming that a substantially fundamental mode has survived at the solitonic power; the minimum pulsewidth was 250 fs at 120 m. For higher input peak powers (110 kW and 190 kW), a second and third soliton are observed at the output: each of them experiences a beam waist reduction. The two or three solitons are generated from a common fission process after a few meters of propagation; the first soliton eventually experiences Raman self-frequency shift up to 2100 nm and it is absorbed; the second and third solitons shift at higher powers, so that they can be eventually observed at the output.

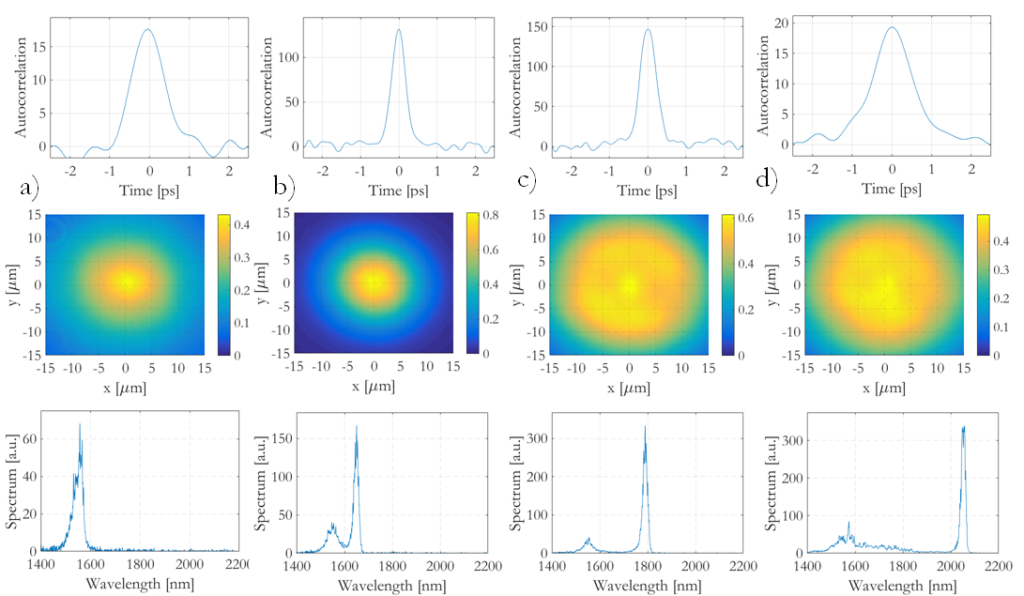
Fig. 2. Measured autocorrelation traces spectra (top row), beam near-field (central row), and spectra (bottom row) after 120 m of fiber transmission, for input pulse peak powers corresponding to: a) 22 kW pre-soliton regime, b) 29 kW soliton regime, c) 37 kW soliton regime with Raman shift, d) 109 kW multiple soliton generation.

4.  Selected publications

Zitelli, Mario, Mangini, Fabio, Ferraro, Mario, Wabnitz, Stefan, “Singlemode spatiotemporal soliton attractor in multimode GRIN fibers”, Photonics Research, in press.

Zitelli, Mario, Mangini, Fabio, Ferraro, Mario, Niang, Alioune, Kharenko, Denis, Wabnitz, Stefan, “High-energy soliton fission dynamics in multimode GRIN fiber,” OPTICS EXPRESS, vol. 28, p. 20473-20488 (2020) 

https://www.osapublishing.org/oe/fulltext.cfm?uri=oe-28-14-20473&id=432976

Mangini, Fabio, Ferraro, Mario, Zitelli, Mario, Niang, Alioune, Tonello, Alessandro, Couderc, Vincent, Wabnitz, Stefan, “Multiphoton-absorption-excited up-conversion luminescence in optical fibers,” PHYSICAL REVIEW APPLIED, vol. 14, p. 1-6 (2020)

https://journals.aps.org/prapplied/abstract/10.1103/PhysRevApplied.14.054063

4.  Related projects

STEMS – Spatiotemporal multimode complex optical systems

5.  References

[1] B. Crosignani and P. D. Porto, “Soliton propagation in multimode optical fibers,” Opt. Lett. 6, 329–330 (1981).

[2] A. S. Ahsan and G. P. Agrawal, “Graded-index solitons in multimode fibers,” Opt. Lett. 43, 3345–3348 (2018).

[3] S.-S. Yu, C.-H. Chien, Y. Lai, and J. Wang, “Spatio-temporal solitary pulses in graded-index materials with Kerr nonlinearity,” Opt. Commun. 119, 167–170 (1995).

[4] S. Raghavan and G. P. Agrawal, “Spatiotemporal solitons in inhomogeneous nonlinear media,” Opt. Commun. 180, 377 – 382 (2000).

[5] M. Karlsson, D. Anderson, and M. Desaix, “Dynamics of self-focusing and self-phase modulation in a parabolic index optical fiber,” Opt. Lett. 17, 22–24 (1992).

[6] T. Hansson, A. Tonello, T. Mansuryan, F. Mangini, M. Zitelli, M. Ferraro, A. Niang, R. Crescenzi, S. Wabnitz, and V. Couderc, “Nonlinear beam self-imaging and self-focusing dynamics in a grin multimode optical fiber: theory and experiments,” Opt. Express 28, 24005–24021 (2020).

[7 ] F. Mangini, M. Ferraro, M. Zitelli, A. Niang, A. Tonello, V. Couderc, and S. Wabnitz, “Multiphoton-absorption-excited up-conversion luminescence in optical fibers,” Phys. Rev. Appl. 14, 054063 (2020).

[8] M. Conforti, C. M. Arabi, A. Mussot, and A. Kudlinski, “Fast and accurate modeling of nonlinear pulse propagation in graded-index multimode fibers,” Opt. Lett. 42, 4004–4007 (2017).

[9] F. Poletti and P. Horak, “Description of ultrashort pulse propagation in multimode optical fibers,” J. Opt. Soc. Am. B 25(10), 1645–1654 (2008).

[10] L. G. Wright, Z. M. Ziegler, P. M. Lushnikov, Z. Zhu, M. A. Eftekhar, D. N. Christodoulides, and F.W. Wise, “Multimode nonlinear fiber optics: Massively parallel numerical solver, tutorial, and outlook,” IEEE J. Sel. Top. Quantum Electron. 24, 1–16 (2018).